2014 Gussage St. Andrews formation








|
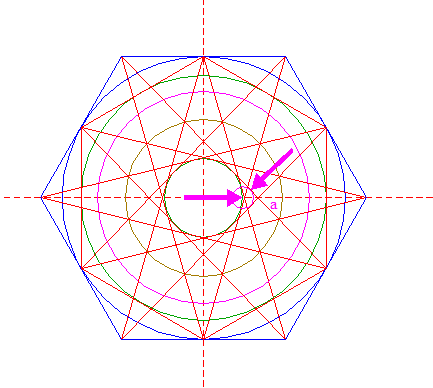
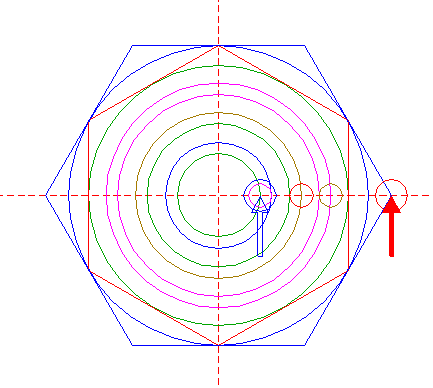
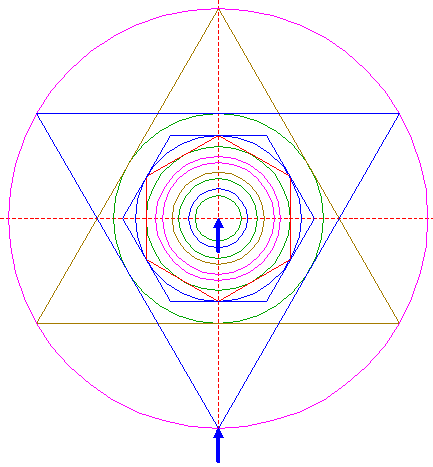
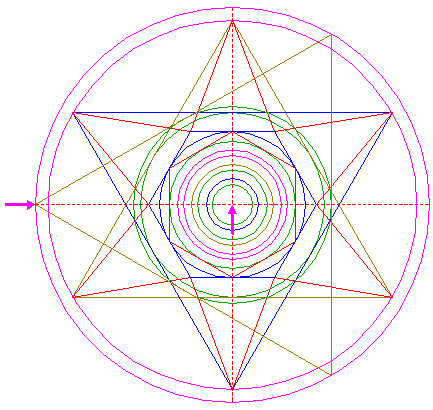
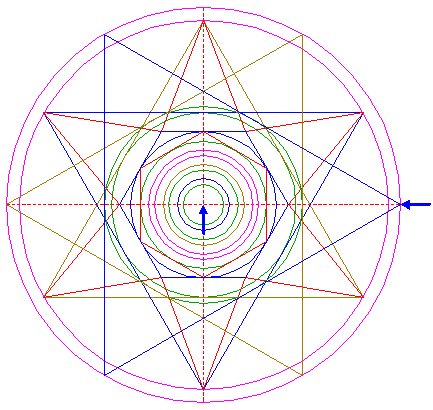
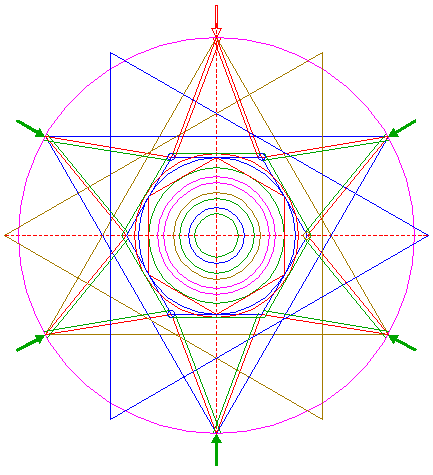
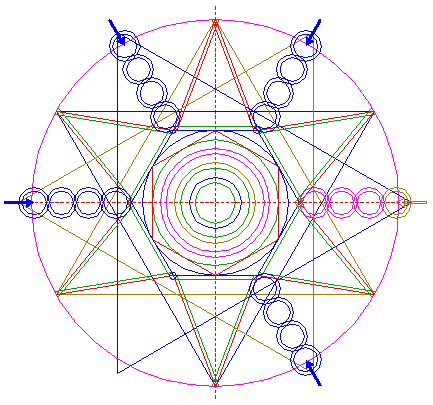
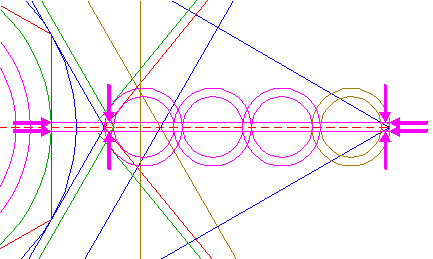
Reconstruction of the 2014 Gussage St. Andrews formation | ||
| 1. | 
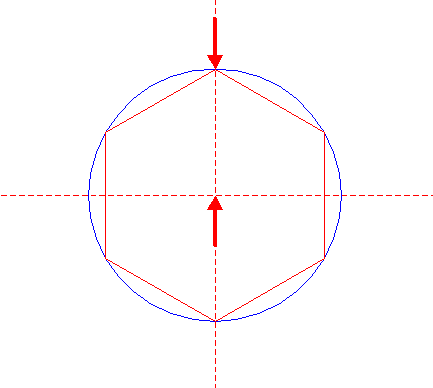
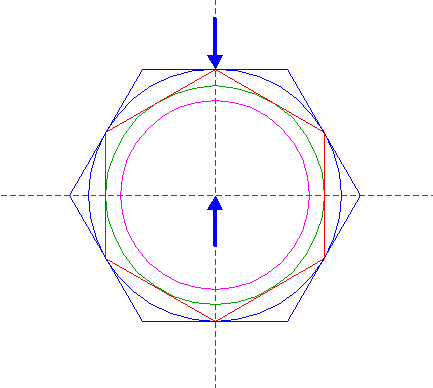
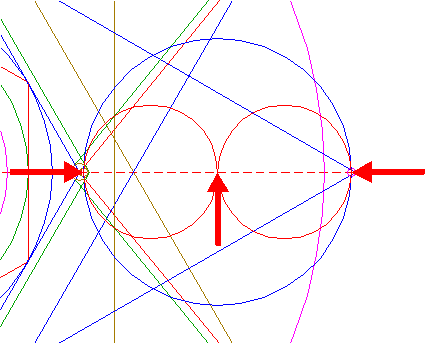
| Draw a circle. Draw and extend the horizontal and vertical centerlines. |
| 2. | 
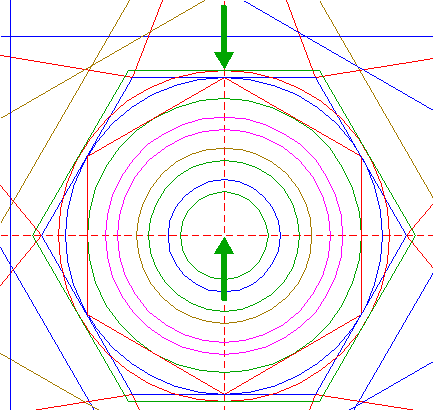
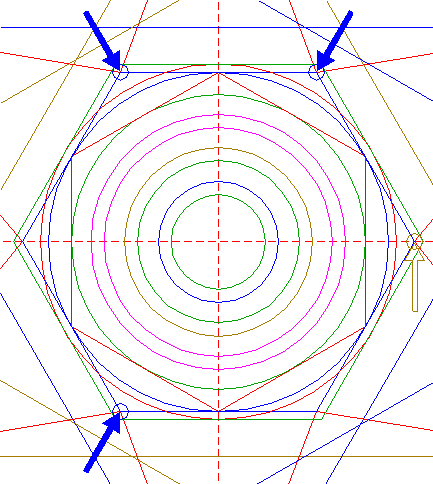
| Construct the inscribed hexagon (regular 6-sided polygon) of circle 1, pointing up. |
| 3. | 
| Construct the inscribed circle of hexagon 2. |
| 4. | 
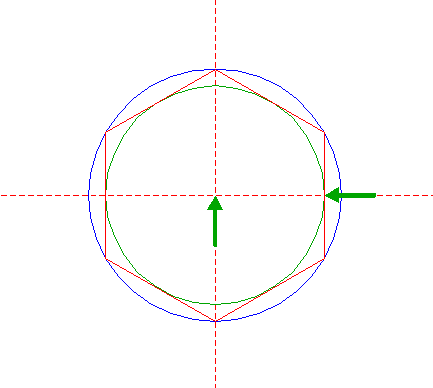
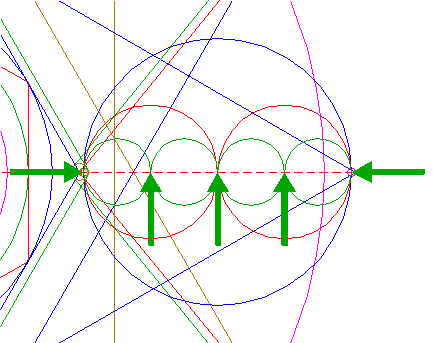
| Construct the inscribed hexagon of circle 3, pointing to the right. |
| 5. | 
| Construct the inscribed circle of hexagon 4. |
| 6. | 
| Construct the circumscribed hexagon of circle 1, pointing to the right. |
| 7. | 
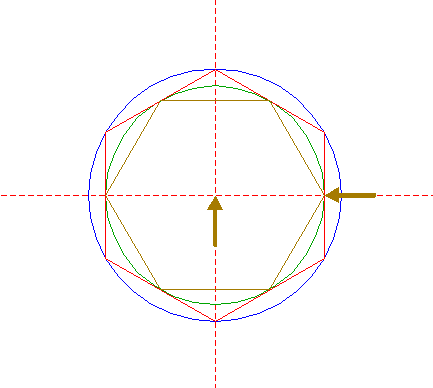
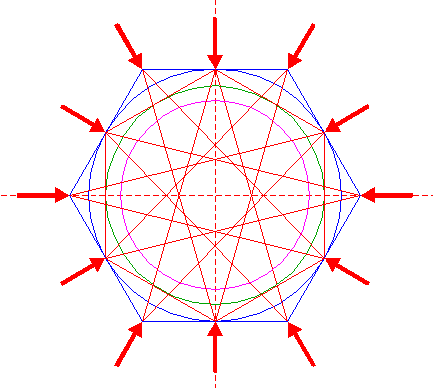
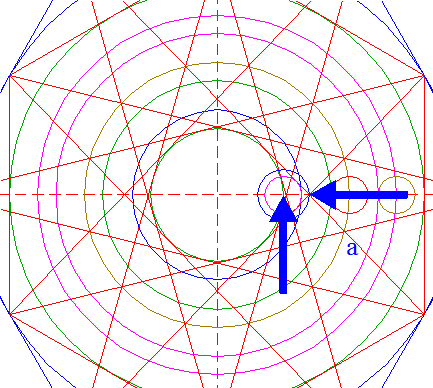
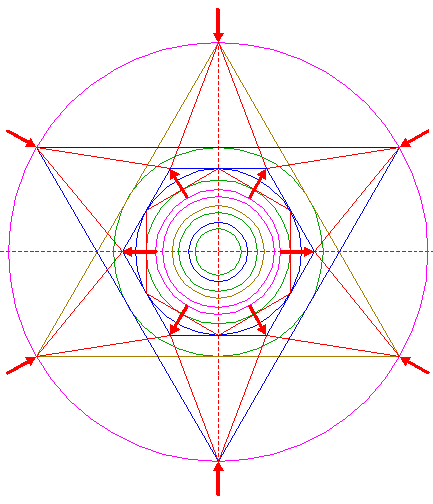
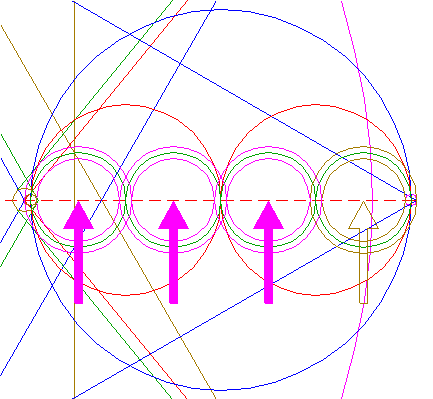
| Draw six pairs of lines, each from a different angular point of hexagon 6 to the two opposite angular points of hexagon 2. |
| 8. | 
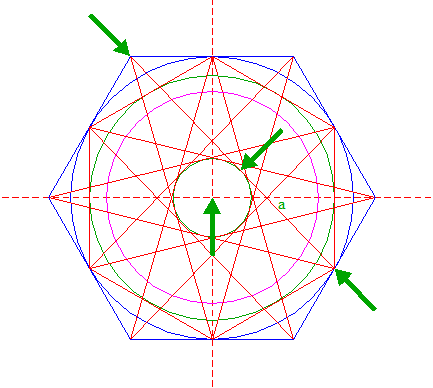
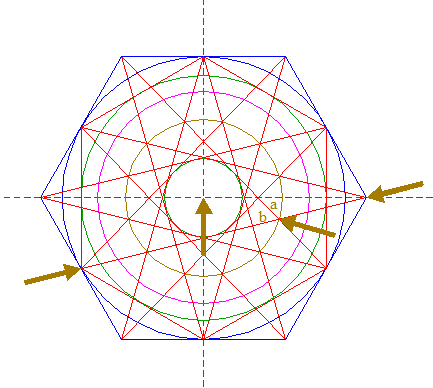
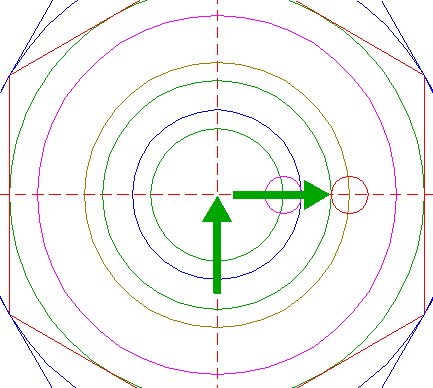
| Define line a, the line 7 from the upper lefthand angular point of hexagon 6 to the lower righthand angular point of hexagon 2. Construct a circle concentric to circle 1, tangent to line a. |
| 9. | 
| Define line b, the line 7 from the righthand angular point of hexagon 6 to the lower lefthand angular point of hexagon 2. Construct a circle concentric to circle 1, passing through the intersection of lines a and b. |
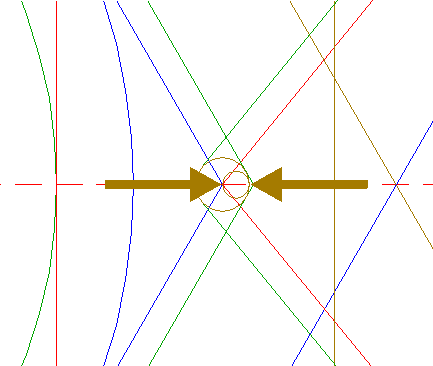
| 10. | 
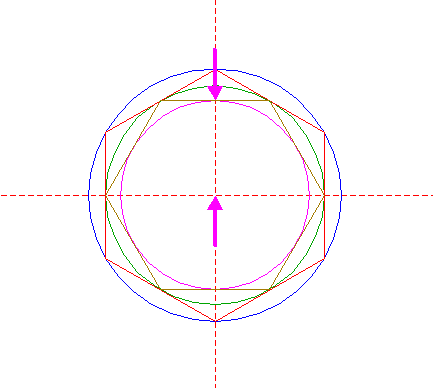
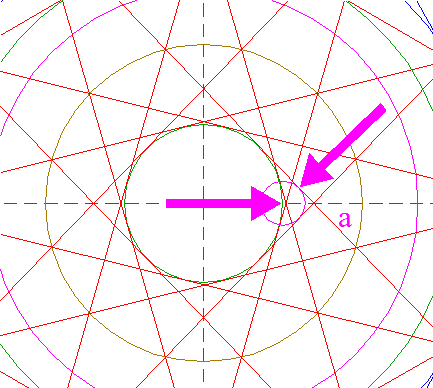
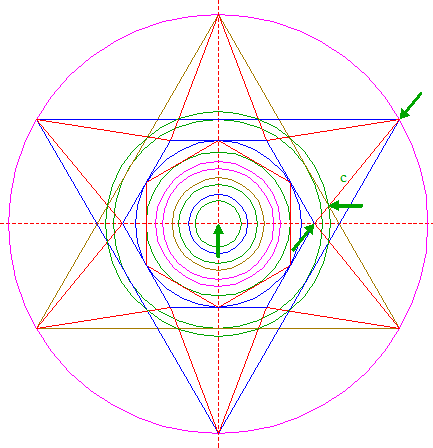
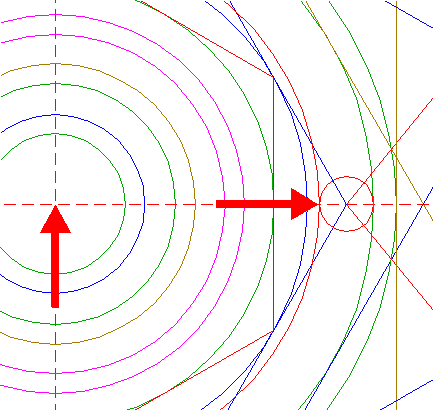
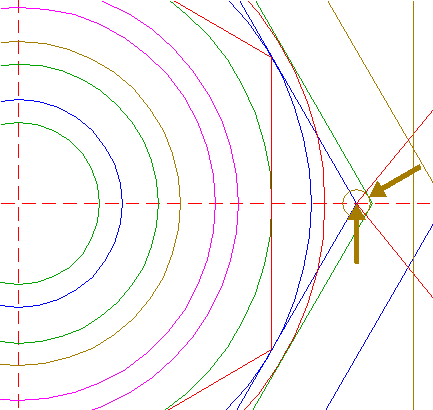
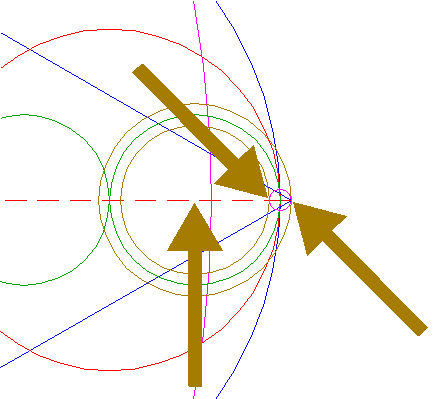
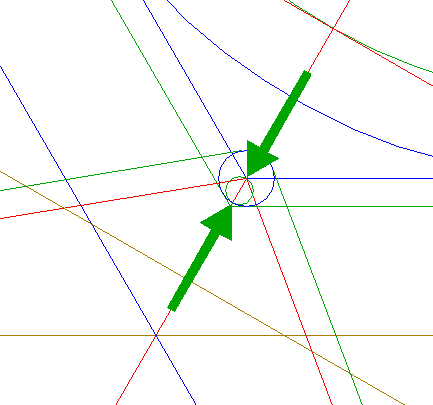
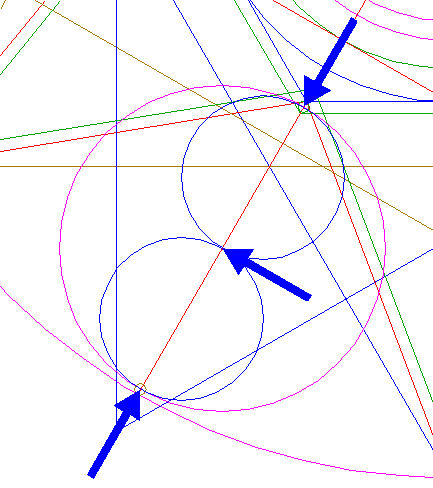
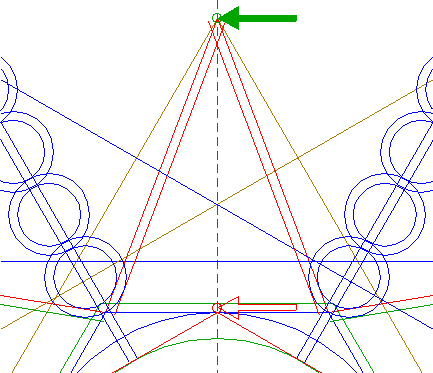
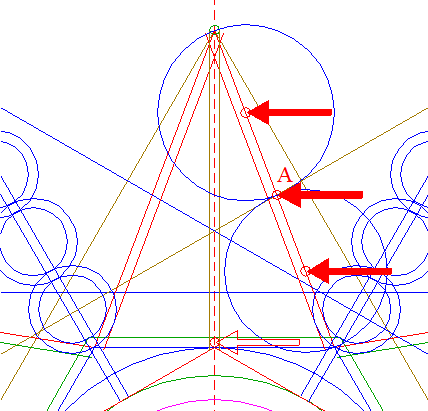
| Construct a circle centered at the righthand intersection of circle 8 and the horizontal centerline, tangent to line a. See detail. |

| ||
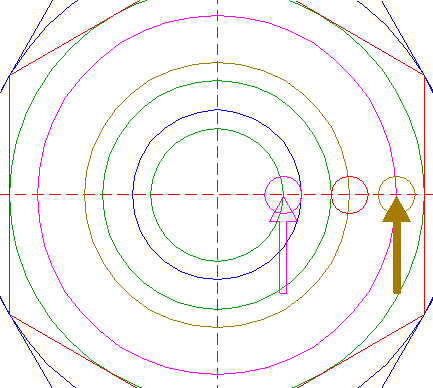
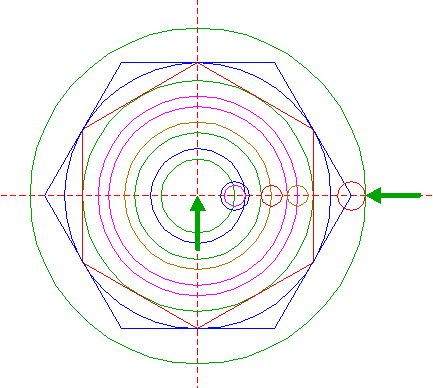
| 11. | 
| Construct a circle concentric to circle 1, tangent to circle 10 at the righthand side. |
| 12. | 
| Copy circle 10 to the righthand intersection of circle 9 and the horizontal centerline. |
| 13. | 
| Construct a circle concentric to circle 1, tangent to circle 12 at the lefthand side. |
| 14. | 
| Copy circle 10 to the righthand intersection of circle 5 and the horizontal centerline. |
| 15. | 
| Construct a circle concentric to circle 1, tangent to circle 14 at the lefthand side. |
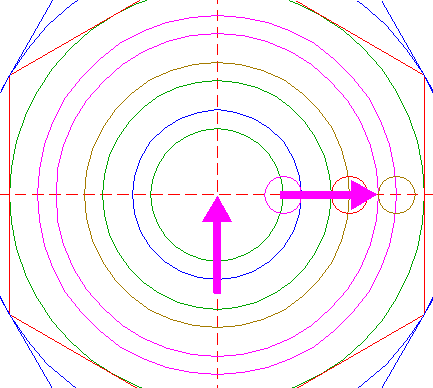
| 16. | 
| Construct a circle concentric to circle 10, passing through the intersection of line a and the horizontal centerline. |
| 17. | 
| Copy circle 16 to the righthand angular point of hexagon 6. |
| 18. | 
| Construct a circle concentric to circle 1, tangent to circle 17 at the righthand side. |
| 19. | 
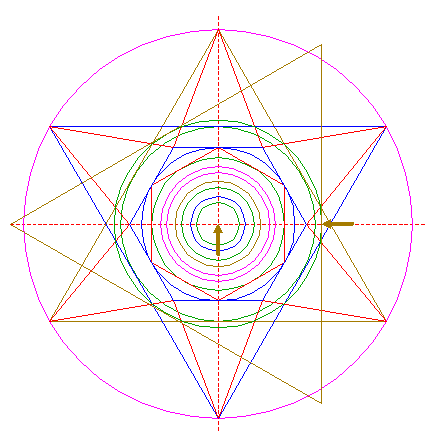
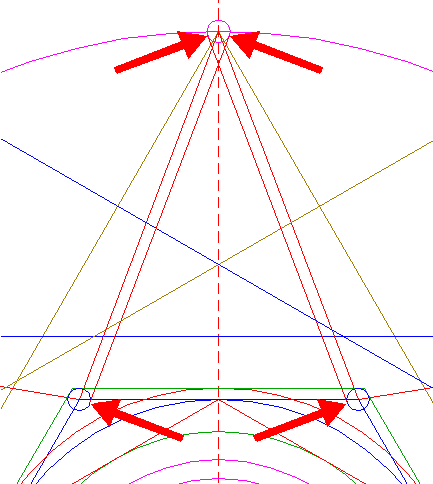
| Construct the circumscribed equilateral triangle of circle 18, pointing up. |
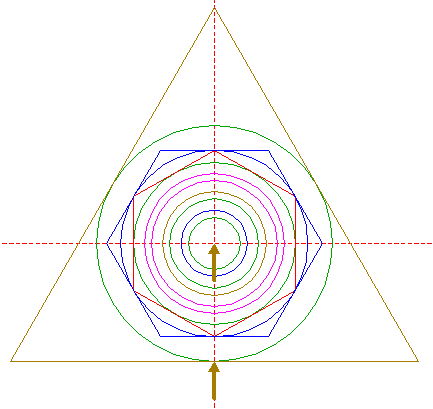
| 20. | 
| Construct the circumscribed circle of triangle 19. |
| 21. | 
| Construct the inscribed equilateral triangle of circle 20, pointing down. |
| 22. | 
| Draw six pairs of lines, each from a different angular point of triangles 19 and 21, to the two nearest angular points of hexagon 6. |
| 23. | 
| Define line c, the line 22 from the upper righthand angular point of triangle 21 to the righthand angular point of hexagon 6. Construct a circle concentric to circle 1, passing through the intersection of the righthand side of triangle 19 and line c. |
| 24. | 
| Construct the circumscribed equilateral triangle of circle 23, pointing to the left. |
| 25. | 
| Construct the circumscribed circle of triangle 24. |
| 26. | 
| Construct the inscribed equilateral triangle of circle 25, pointing to the right. |
| 27. | 
| Construct a circle concentric to circle 1, tangent to circle 17 at the lefthand side. |
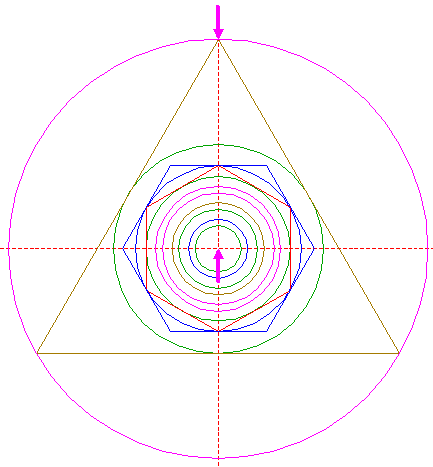
| 28. | 
| Construct the circumscribed hexagon of circle 27, pointing to the right. |
| 29. | 
| Construct a circle centered at the righthand angular point of hexagon 6, tangent to the upper righthand side of hexagon 28. |
| 30. | 
| Copy circle 29 to the top of triangle 19. |
| 31. | 
| Copy circle 29 to the upper lefthand and righthand and to the lower lefthand angular points of hexagon 6. |
| 32. | 
| Construct two lines, parallel to the upper two lines 22 at the inner sides, tangent to circle 30 and upper circles 31, as shown. |
| 33. | 
| Repeat step 32 (and all necessary previous steps) five times, with respect to the other angular points of triangles 19 and 21. |
| 34. | 
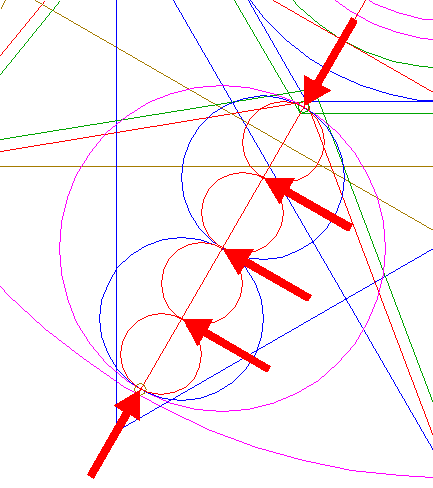
| Construct a "two-points" circle (defined by the two end-points of a centerline) between the center of circle 29 and its righthand intersection with the horizontal centerline. |
| 35. | 
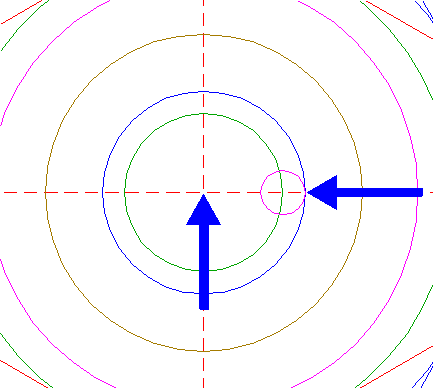
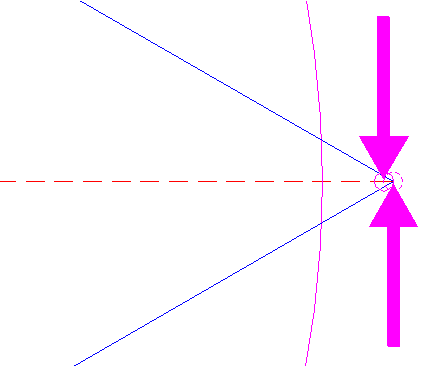
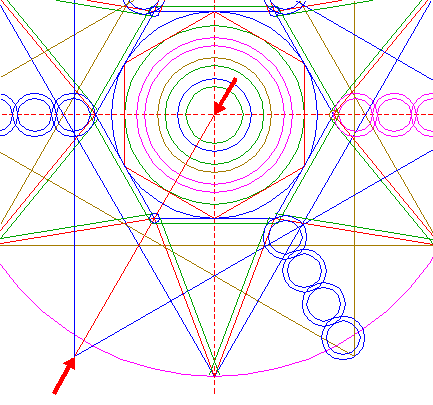
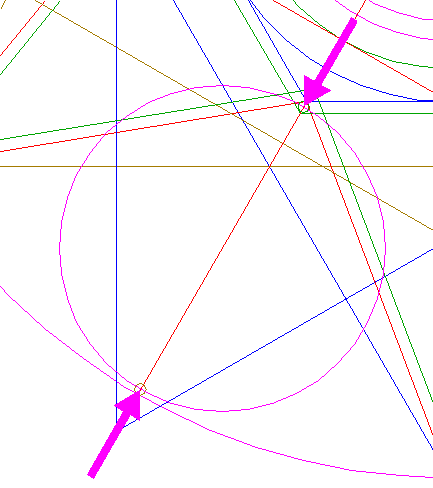
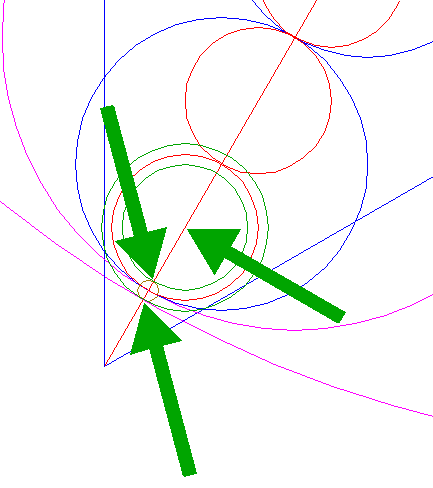
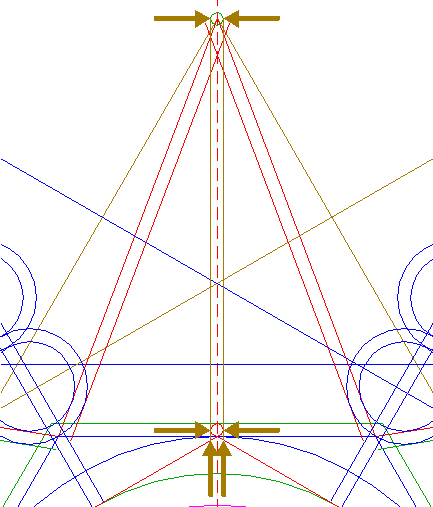
| Copy circle 34 to the righthand angular point of triangle 26, and move this circle (copy and delete original) to its own lefthand intersection with the horizontal centerline. See detail. |

| ||
| 36. | 
| Construct a "two-points" circle between the centers of circles 34 and 35. |
| 37. | 
| Construct two "two-points" circles between the center of circle 36 and the centers of circles 34 and 35 respectively. |
| 38. | 
| Construct four "two-points" circles, two between the center of lefthand circle 37 and its intersections with the horizontal centerline, the other two similar with respect to the righthand circle 37. |
| 39. | 
| Construct two circles concentric to the righthand circle 38, tangent to circle 35 at both sides. |
| 40. | 
| Copy circles 39 three times, to the centers of the other circles 38. |
| 41. | 
| Repeat steps 39 and 40 (and all necessary previous steps) four times, with respect to the upper lefthand angular point of triangle 26 and the angular points of triangle 24. |
| 42. | 
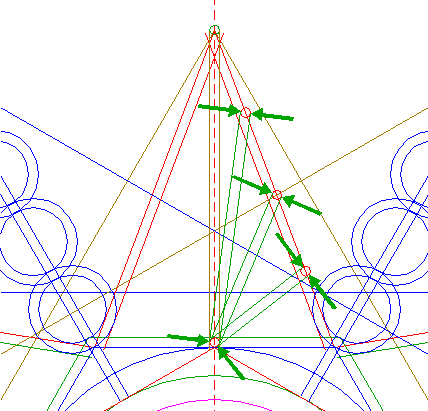
| Draw the connecting line between the center of circle 1 and the lower lefthand angular point of triangle 26. |
| 43. | 
| Construct a "two-points" circle between the center of lower circle 31 and its lower intersection with line 42. |
| 44. | 
| Copy circle 43 to the intersection of circle 20 and line 42. Move this circle to its own upper intersection with line 42. |
| 45. | 
| Construct a "two-points" circle between the centers of circles 43 and 44. |
| 46. | 
| Construct two "two-points" circles between the center of circle 45 and the centers of circles 43 and 44 respectively. |
| 47. | 
| Construct four "two-points" circles, two between the center of upper circle 46 and its intersections with line 42, the other two similar with respect to the lower circle 46. |
| 48. | 
| Construct two circles concentric to the lowest circle 47, tangent to circle 44 at both sides. |
| 49. | 
| Copy circles 48 three times, to the centers of the other circles 47. |
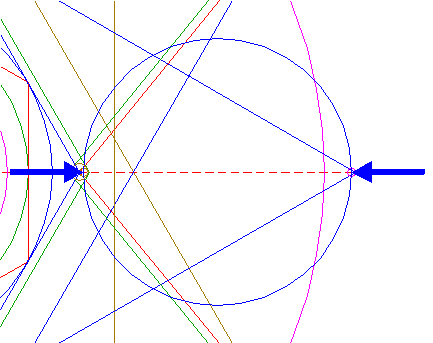
| 50. | 
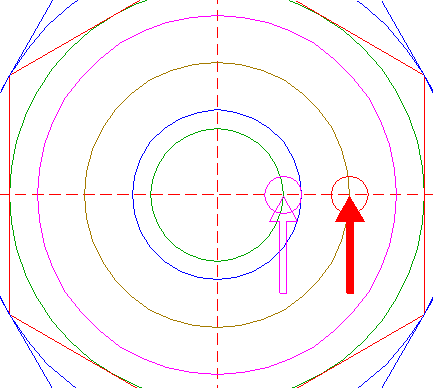
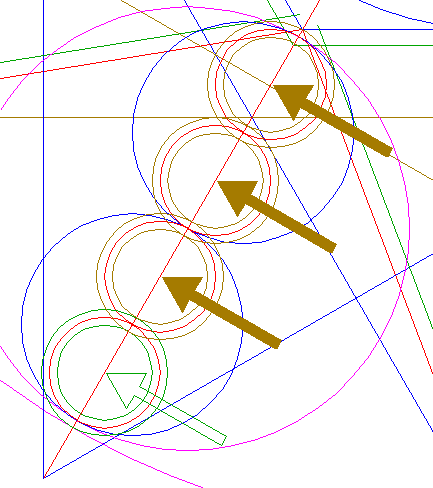
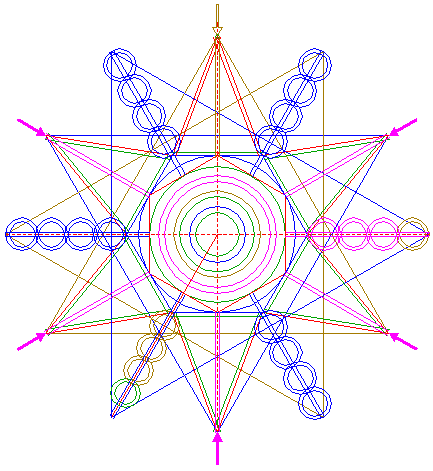
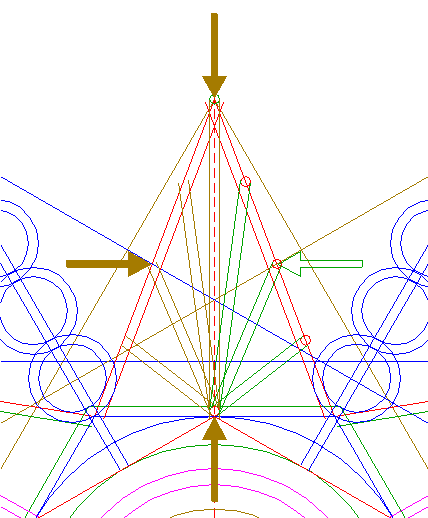
| Construct two parallel lines, tangent to circles 34 and 35 at both sides. Extend these lines to the left upto hexagon 2, and to the right upto the outer circle 39. See detail. |

| ||
| 51. | 
| Repeat step 50 (and all necessary previous steps) five times, with respect to the other angular points of triangles 24 and 26. |
| 52. | 
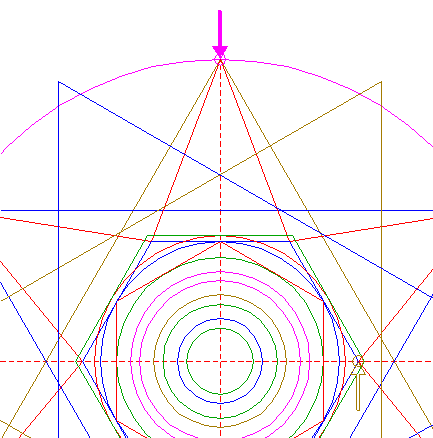
| Construct a "two-points" circle between the intersections of the upper sides of hexagons 6 and 28 with the vertical centerline. |
| 53. | 
| Copy circle 52 to the top of triangle 19. |
| 54. | 
| Construct two parallel lines, tangent to circles 52 and 53 at both sides. Extend these lines downto hexagon 2. |
| 55. | 
| Repeat step 54 (and all necessary previous steps) five times, with respect to the other angular points of triangles 19 and 21. |
| 56. | 
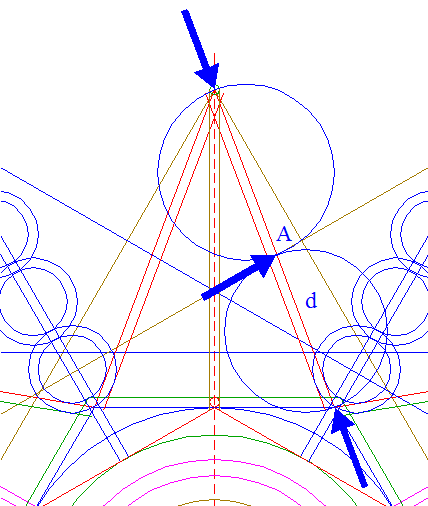
| Define line d, the line 22 from the top of triangle 19 to the upper righthand angular point of hexagon 6. Point A is the intersection of line d and the upper lefthand side of triangle 24. Construct two "two-points" circles, between point A and the end-points of line d respectively. |
| 57. | 
| Copy circle 52 three times, to point A, and to the centers of circles 56. |
| 58. | 
| Construct three pairs of parallel lines, all tangent to circle 52 and tangent to circles 57 respectively, all at both sides. |
| 59. | 
| Copy lines 58, while mirroring with respect to the vertical centerline. |
| 60. | 
| Repeat steps 58 and 59 (and all necessary previous steps) two times, with respect to the other angular points of triangle 19. |
| 61. | 
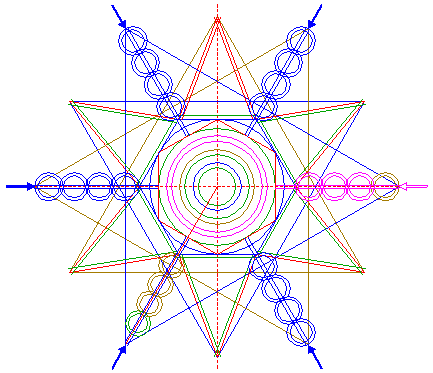
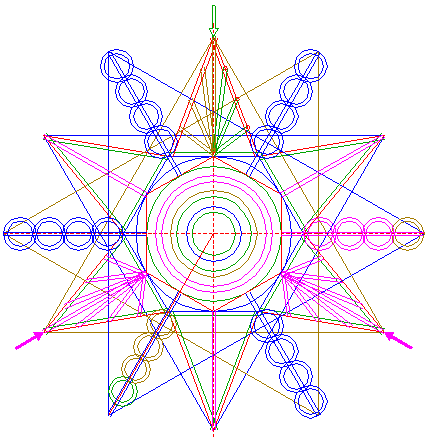
| Circles 5, 8, 9, 11, 13, 15, 39, 40, 41, 48 and 49, hexagons 2, 6 and 28, and lines 22, 32, 33, 50, 51, 54, 58, 59 and 60, are used for the final reconstruction. |
| 62. | 
| Remove all parts not visible within the formation itself. |
| 63. | 
| Colour all areas corresponding to standing... |
| 64. | 
| ...or to flattened crop, and finish the reconstruction of the 2014 Gussage St. Andrews formation. |
| 65. | 
| The final result, matched with the aerial image. |
| Copyright © 2014, Zef Damen, The Netherlands |