BACK TO BASICS
The internal geometry of crop circles
Wat maakt graancirkels zo'n fascinerend fenomeen. Natuurlijk zal het onverklaarbare aspect een grote rol spelen. Maar is dat alles? Hoe komt het toch dat mensen al ge´nteresseerd raken als ze alleen nog maar de pictogrammen hebben gezien. Als ze nog niets weten van de verdere achtergrond. Wat maakt het dat de symbolen zo'n sterke uitwerking hebben op mensen.
Deze vragen spelen al jaren door mijn hoofd. Er is iets met de pictogrammen dat een soort hypnotiserende uitwerking op mensen heeft. De vormen zijn zodanig dat ze je aangrijpen, maar waarom.
Al vanaf de eerste graancirkel zijn er mensen geweest die zich met de geometrie hebben beziggehouden. Bijvoorbeeld John Martineau en Wolfgang Schindler. Zij richtten zich vooral op de 'buitenkant' van de pictogrammen. Tot 1992 waren vele pictogrammen in te passen in vijfvoudige geometrie. In 1992 veranderde de vormen en was het gedaan met de werkwijze van hen. Later heeft Gerald Hawkins intensief onderzoek gedaan naar verschillende elementen binnen crop circles. Hierbij vond hij ondermeer sterke aanwijzingen voor het bestaan van diatonische ratio's in pictogrammen.
Hoewel al deze resultaten fascinerend zijn, waren ze voor mij niet voldoende. Er moest meer zijn. Een fundamentelere grondslag. En ik heb hem gevonden. Veel crop circles bevatten een eenvoudige, maar zeer verhelderende geometrie. Een geometrie die de bevindingen van Martineau, Schindler en Hawkins als resultaat heeft. De bron, de oorzaak is van hun bevindingen. De interne geometrie van graancirkels.
Het boek waarin deze fundamenten grondig wordt beschreven zal over enige tijd uitkomen. De kern zal hier nader worden toegelicht.
Het begon allemaal met mijn pogingen om bestaande formaties op papier te reconstrueren met alleen een passer en een liniaal, waarbij de liniaal alleen werd gebruikt om rechte strepen te kunnen trekken. Niet om mee te meten. Dus echte zuivere constructie.
De resultaten waren fascinerend:
1. Alle door mij onderzochte formaties hebben hetzelfde basispatroon.
2. Elk element uit een formatie is niet toevallig, maar een strikt resultaat van de constructie (dus ook de onderlinge verhoudingen).
3. De noodzakelijke constructiepunten (centra van gebruikte cirkels) liggen nooit in rechtopstaand graan.
Hoe werkt het.
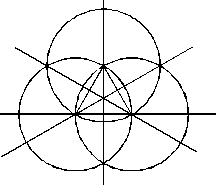
Het genoemde basispatroon ziet er alsvolgt uit

Vanuit dit patroon zijn vele formaties te construeren. In het boek wordt beschreven hoe dit basispatroon moet worden gemaakt.
Laten we eens een formatie proberen, een relatief eenvoudige. Bijvoorbeeld de Harlequin formatie van 1997.
Via enkele eenvoudige constructiestappen komen we bij het volgende diagram:
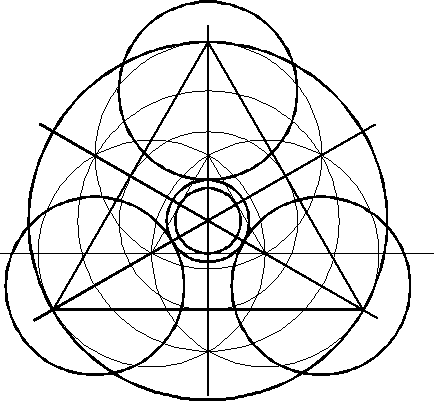
In het diagram is een gelijkzijdige driehoek te zien.
Deze is geconstrueerd in de drie cirkels die nodig zijn om het basisfiguur te maken en is dezelfde die ook in de formatie te zien is. Zie dat er een cirkel precies passend in de driehoek is gecontrueerd. Dit is dezelfde cirkel als de drie die op de hoeken zijn geconstrueerd. Toeval ??
De binnenste cirkel in de formatie past precies in de gelijkzijdige driehoek van het basisfiguur. Toeval ??
Het eindresultaat ziet er als volgt uit:

Nu is dit een relatief eenvoudig en voor de hand liggend figuur. Bij de volgende ligt dit al anders. Uitgaande van hetzelfde basisfiguur kunnen we via een kleine vijftien constructie stappen het volgende maken:
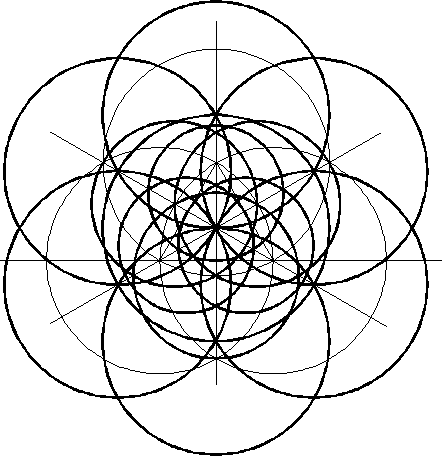
Dit lijkt een brij aan strepen en cirkels, maar is echter de interne geometrie van het volgende pictogram:

Ondanks het compexe karakter van het pictogram, kan het worden geconstrueerd zonder 'het graan plat te stampen'. Het volgende diagram laat zien waar de noodzakelijke constructiepunten liggen. Allemaal in platgelegd graan.
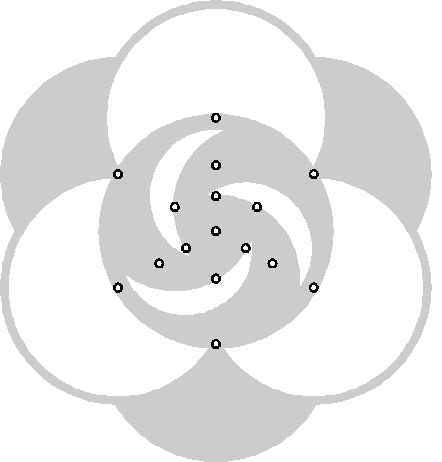
Duidelijk is te zien dat een aantal punten precies op de rand met het staande graan ligt. Het past precies. Was de centrale cirkel bijvoorbeeld iets kleiner geweest, dan had het figuur niet gemaakt kunnen worden zonder in het staande graan te staan. Maar 'gelukkig' is de centrale cirkel precies groot genoeg. Toeval ??
Dit geldt ook voor het volgende pictogram. Uitgaande van het basisfiguur komen we onder andere via it bij
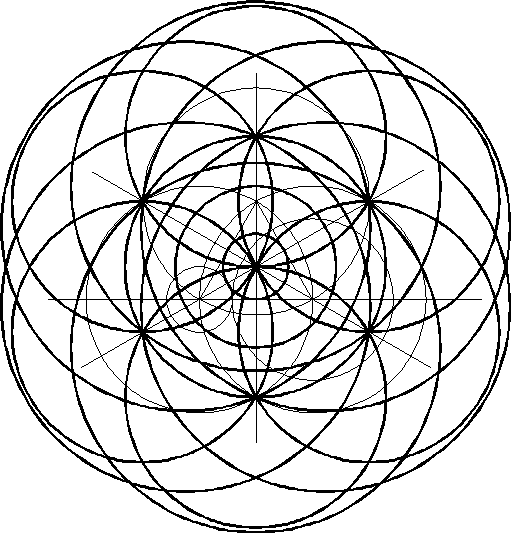
Ook hier liggende de constructiepunten precies op de rand.

Was de de binnenste cirkel van rechtopstaand graan iets groter geweest, had het figuur niet gemaakt kunnen worden, zonder graan te beschadigen. Maar ook hier geldt weer dat hij net 'de goede maat' heeft. Toeval ??
Bij de formatie van Etchilhampton uit 1997 gaat het nog verder.
Via vele stappen komen we bij het uiteindelijke figuur, waarbij de constructiepunten alsvolgt liggen
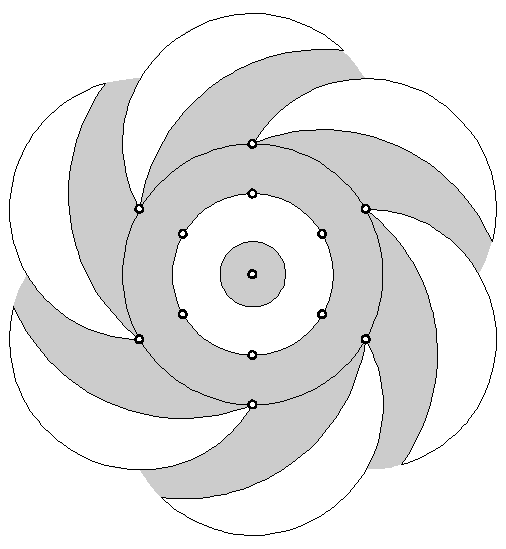
Om het figuur te kunnen construeren zijn een aantal punten nodig die relatief ver van het centrum liggen. Dit had een probleem gevormd als daar niet juist een ring had gelegen. Toeval ??
In de formatie zelf ligt het buitenste punt ook nog net in het 'platte' graan. Toeval ??
Gaat het nu alleen om de constructiepunten?
Nee. Deze punten zijn slechts 1 van de vele indicatoren die erop wijzen dat de formaties volgens een zeer precies geometrisch patroon tot stand komen. Ze worden gemaakt doormiddel van ons bekende geometrische principes.
Wat kunnen we hier nu mee? Wat vertelt het ons?
Doordat ze allemaal gemaakt kunnen worden met dezelfde basisfiguur, kunnen ze ook met elkaar vergeleken worden. Bijvoorbeeld wat hun grootte betreft. Ze kunnen aan de hand van dit basisfiguur 'op elkaar geprojecteerd' worden.
Omdat de interne geometrie nu bekent is, zijn ze driedimensionaal te maken in hun pure vorm.
Zoals aan de basisfiguur te zien is, zijn ze allemaal gebaseerd op een gelijkzijdige driehoek. Een driedimensionale gelijkzijdige driehoek is een tetrahedron. Dit zal veel mensen bekend en als muziek in de oren klinken. De pictogrammen zijn met behulp van bovenstaande geometrie om te zetten in drie dimensionale figuren die gebaseerd zijn op zuivere tetrahedrons!
Elk element in een formatie is door de geometrie per definitie gerelateerd aan elk ander element binnen de formatie. Diatonische ratio's zijn hiervan het logische gevolg. Maar het gaat verder. Elk element van de ene formatie kan worden gerelateerd aan elk willekeurig element van een andere formatie.
Tot nu toe is alleen gekeken naar zesvoudige geometrie. Wat nu met vijfvoudige geometrie, bijvoorbeeld die van de Star of Bethlehem uit 1997.
Met behulp van het basisfiguur is alsvolgt tot vijfvoudige geometrie te komen
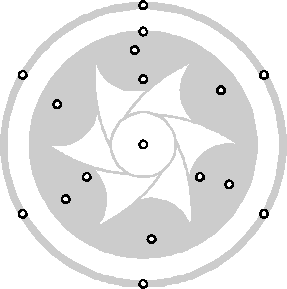
Van hieruit is via een aantal constructie stappen het volgende figuur te maken
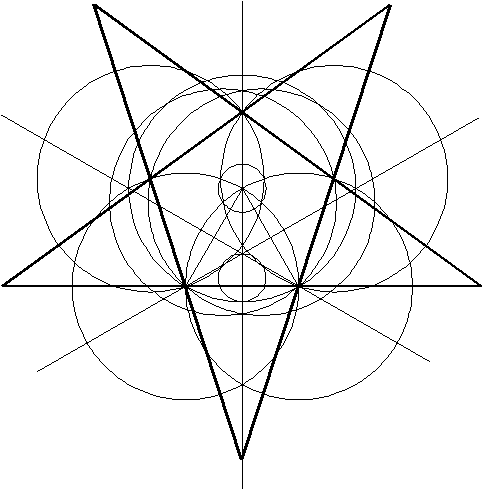
Hetgeen direkt leidt tot:
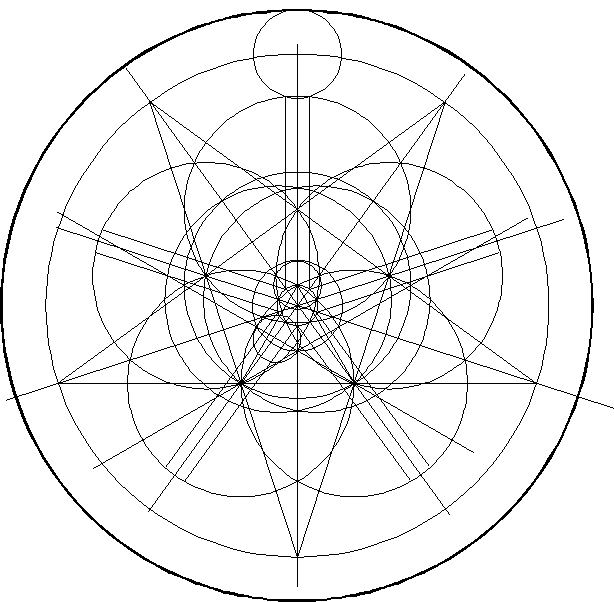
Ook hier geldt dat de formatie dusdanig is dat alle constructiepunten 'binnen' de figuur vallen.
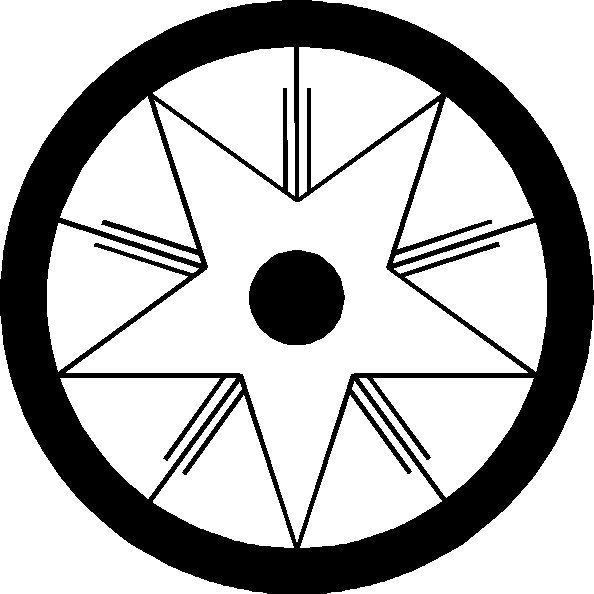
De binnenste cirkel had geen inch kleiner mogen zijn, of we hadden weer een probleem gehad. Toeval ??
Dit is slechts een greep uit de fascinerende wereld van interne crop circle geometrie. Mijn bevindingen gaan veel verder dan hier beschreven kan worden. Zo is bijvoorbeeld aan te tonen dat de 'Web' bij Avebury een samenspel is van vijfvoudige en zesvoudige geometrie. Ze werken in deze formatie heel nauw samen. Ze zijn 'interlocking'.
Misschien dat deze perfecte geometrie verder niets zegt. Dat zij alleen maar een noodzakelijkheid is om de pictogrammen harmonisch te maken, waardoor ze de geconstateerde 'hypnotiserende' uitwerking op mensen heeft.
Misschien is het feit dat de constructiepunten nooit in het staande graan liggen met opzet gedaan om aan te geven dat we op de goede weg zitten met deze vorm van geometrische analyse.
In mijn binnenkort te verschijnen boek wordt een uitgebreide analyse van vele formaties gemaakt. Hierin wordt gewezen op een onwaarschijnlijke reeks van 'toevalligheden'. Niet alleen van constructiepunten, maar ook van de meest onwaarschijnlijke snijpunten en verhoudingen binnen formaties.
Meer informatie is op te vragen via email:
Email:- Bert Janssen,1997