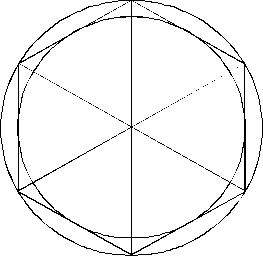
Hackpen Hill 1999
Bert Janssen
The 1999 Hackpen Hill formation was definitely one of the most intriguing crop circles of this season. From the very moment of its appearance everyone seemed to be caught by its pattern: a pattern that seemed to be consisting mainly of overlapping and/or touching spirals. And a pattern that - according to many - would be taking a lot of thought before actually being deciphered.
Which turned out to be true... It took me quite a while before I had figured out how this formation worked. I tried every possible spiral, but with no satisfactory result.
Then, all of a sudden, it dawned to me. It's not made of spirals, it's made of circles!
From that moment on, things became quite easy. The whole geometry of the formation even turned out to be ridiculously simple!
This is how it works.
The basis is formed by a hexagon with a circle around it and a circle within.

This basic hexagon can be constructed by means of the 'basic figure' that I showed in my article "Back to Basics".
We now construct the next four circles:
1.
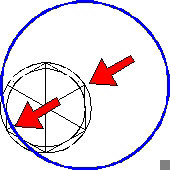
The first circle has its centre on one of the angular points of the hexagon (see right arrow), and touches the inner circle (see left arrow).
2.
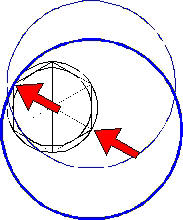
This second circle has its centre on the next angular point of the hexagon (see right arrow), and it crosses the opposite angular point (see left arrow).
3.
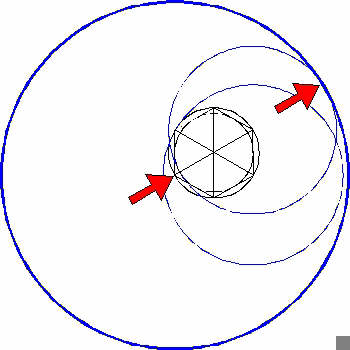
The third circle has its centre on the angular point opposite of the centre of the first circle (see left arrow). This third circle touches the first circle as shown in the diagram.
4.
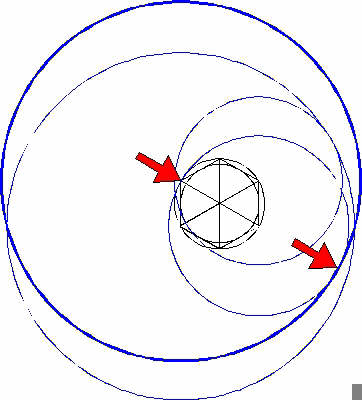
We now construct a fourth circle in exactly the same way we constructed the third circle. This time however, we take the second circle as our starting point.
(See diagram).
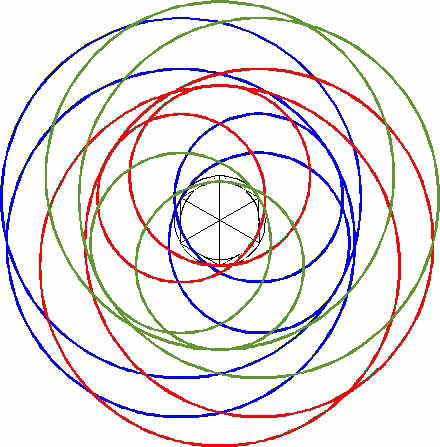
This set of four circles can be constructed again. While doing that, we shift all of the centres exactly two angular points (120 degrees).
In the same manner we can construct a third set of four circles, by which we have covered all of the angular points of the hexagon.
The next diagram shows the result.
(Every set of four circles has its own colour).
(
Per set of four circles we only have to construct one fifth circle in order to complete the lot. In order to do this, we have to return to the central hexagon. In this hexagon we construct a hexagram. Within this hexagram we once again construct a hexagram (see diagram):
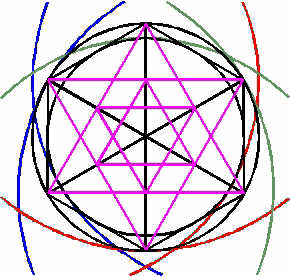
The necessary circles can be constructed in the following way:
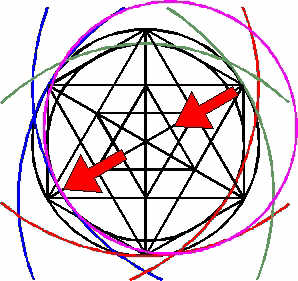
The fifth circle (that belongs to the four circles of the blue set) has its centre point on the intersection that's been indicated by the right arrow. The circle touches the inner circle of the hexagon, as indicated by the left arrow.
In exactly the same way we can construct the fifth circle of the green set and the fifth circle of the red set.
We have now constructed every necessary circle.
The total result looks as follows:
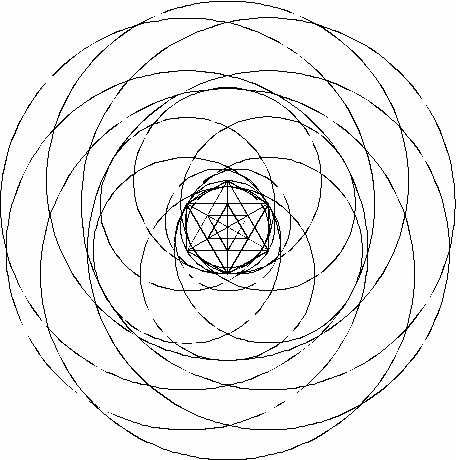
By taking the correct parts of the circles, we get the following diagram:
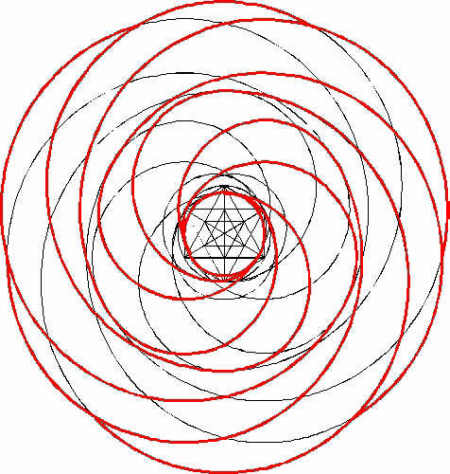
This diagram forms the principle of the 1999 Hackpen Hill formation. At first sight it doesn't seem to be entirely correct, since there are no overlapping and/or touching 'spirals'. The red lines however show us the middle of the various pathways. By broadening these lines, by giving them the actual size of the pathways, we create the following figure:

All of a sudden we see overlapping and/or touching 'spirals'.
In other words:
The 1999 Hackpen Hill formation is not constructed out of spirals, but out of circles.
One should notice that this formation seems to be based on three-fold geometry; in reality however, it is based on six-fold geometry, as can be deducted from the above analysis.
In a future article I will analyse a few other 1999 formations.
I will then try to show what those formations would look like if they were three-dimensional. In order to give you a taste of what I mean, I transformed a fantasy dumb-bell into a three-dimensional figure (see diagrams).
|
|
|
|
Text and diagrams: Bert Janssen, (c) 1999
Copyright: Bert Janssen, 1997