For the past year, Professor Hawkins - mathematician, astronomer, archaeoastronomer, and author (Stonehenge Decoded, Beyond Stonehenge ) - has let stand his challenge to an international cadre of mathematicians, as well as to a quarter-million readers of Science News, to come up with the Fifth Crop Circle Theorem he uncovered through his studies of these incredible Formations. NO ONE successfully met his challenge.
The only clue Dr Hawkins offered was that Theorem Five was a general one from which four others, all of which he had previously discovered through his mathematical Circles analyses, might be derived. The challenge was to wrap one's brain around a theorem which hadn't yet 'been born' into our reality, state it, and prove it using Euclidean methods.
Dr Hawkins discovered all five Euclidean hypotheses by carefully analysing the relationships between the areas and diameters of the Circles and Rings as they occurred within the Formations. The previously published four theorems dealt with the relationships of the areas of regular polygons and their inscribed and circumscribed circles (reprinted below).
A circumscribed circle is one which encloses and contacts a regular polygon's angles. Imagine a triangle with three equal sides, then draw a circle around it such that the circle's radius is the distance between the centre point of the triangle and an apex. By using the same centre but decreasing the radius so that the circle's circumference touches each of the inner-aspects of the triangle's sides, one draws its inscribed circle.
Since the professor issued his challenge, the time he allotted for feedback from math students and teachers is now up, and as he promised he would, he's let us in on his secret ...
Dr Hawkins' point in withholding the Fifth Theorem was to emphasise how difficult it is to realise a new one. Once a theorem is stated, it is relatively easy to 'prove'. Being the first to come up with a 'new' theorem is the hard part!
The Fifth Theorem, according to Dr Hawkins, fits into Euclid's thirteenth book of his three-volume Elements tome, "somewhere after Proposition 12" - yet Euclid had not included it. Nor was the professor able to locate any of these Crop Circle Theorems in any mathematics text or reference book, ancient or modern!
"What sort of intellectual/psychological profile is needed," wondered Dr H, "to understand those who go one step further than Euclid? And for what purpose are our Circles designed?"
What has occurred because of the Crop Circles and Dr Hawkins' insightful study of them is quite extraordinary :
These Five Circle Theorems had not been integrated into human understanding until the CircleMakers shone their Lights (as it were ;-) upon these Patterns in our fields. Under the patient tutelage of the CircleMakers, Dr H slowly came to recognise these esoteric mathematical Truths - which, in fact, most of the Patterns hold. His lessons, admits the good doctor, were ongoing throughout the day: while he was showering, while driving and eating ...
In still other words: As a direct result of the Crop Circles' arrivals, five new mathematical truths have been added to the geometer's lexicon.
As does Dr Hawkins, I know that many of us also delight in pondering the Question of Questions: Who, indeed - and Why! - are our CircleMakers?! ;-)
The next two paragraphs are paraphrased from SCIENCE NEWS ONLINE, October 12, 1996.
Crop Circles: Theorems in Wheat Fields - by G Hawkins, PhD [brackets are my additions]
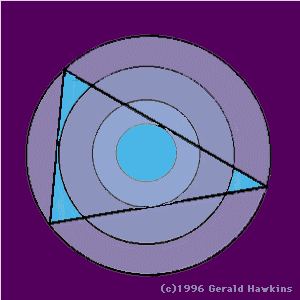
"... Hawkins found that he could use the principles of Euclidean geometry to prove four theorems derived from the relationships among the areas depicted in these Crop Circle patterns [refer to graphic A]. He also discovered a fifth, more general theorem, from which he could derive the other four. Hawkins' Fifth Crop Circle Theorem involves a triangle and various concentric circles touching the triangle's sides and corners [see graphic B]. As the mathematical relationships of the Circles and Rings are explored using various triangles [i.e., equilateral, isosceles, right], the special Crop Circle geometries are revealed. The different triangles disclose different geometrical relationships.
An equilateral triangle produces one of the observed Crop Circle patterns [the one which arrived in 1993, on the Hogsback between Farnham and Guildford in Hampshire - see graphic]; three isosceles triangles reveal additional Crop Circle geometries ... "

For completeness, I've included the first four theorems Professor Hawkins derived from his Circle studies. I regret that I do not currently have the graphics available for them, am working toward obtaining them and having them uploaded.
The ratio of the diameter of the triangle's circumscribed circle to the diameter of the circles at each corner is 4:3.
The Pattern consists of these 3 Circles not quite touching, with the following geometry overlaying it: Connect the centres of the bottom 2 circles with a straight line, then join the left and top centres, and finally the right and top ones. This is the triangle referred to. Now, find the centre of the triangle and using it, draw a circle on top of these three such that its circumference passes through the centres of each of the 3 circles. This fourth circle is the triangle's circumscribed circle. Referring again to the theorem: The ratio of the diameter of this fourth circle to the diameters of each of the others is 4:3.
(Is that neat, or What?! But there's even more magic here: each of 3 tangents drawn between the three circles is tangent to each of the 3 circles - that's the kind of precision that regularly happens in our fields, even on moonless nights! It would take too long for me to try to describe these tangents precisely enough for you to draw them, but I'm trying to obtain a scanned copy of this graphic.)
(re: an equilateral triangle with a circumscribed and
inscribed circle)
For an equilateral triangle, the ratio of the areas of the circumscribed and inscribed
circles is 4:1. The area of the ring between the circles (the annulus) is 3 times the area
of the inscribed circle.

(re: a square with circumscribed and inscribed circles)
For a square, the ratio of the areas of the circumscribed and inscribed circles is 2:1.
If a second square is inscribed within the inscribed circle of the first, and so on to the
mth square, then the ratio of the areas of the original circumscribed circle and the
innermost circle is 2-to-the-m:1.
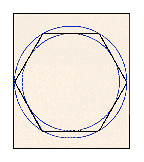
(re: a hexagon with circumscribed and inscribed circles)
For a regular hexagon, the ratio of the areas of its circumscribed and inscribed circle
is 4:3.
Theorems I, II, and IV all deal with 4:3 ratios. (Even in writing it just now, I see that I, II, and IV = [I+II=III] and IV.) In last year's Julia Set at the Stonehenge, all flanking Circles along the 'spine' were evenly balanced (one inside the phi curve one outside it, two and two, three and three) - except in one case, where there were 3 smaller Circles on the inside, but 4 Circles on the opposite side ...
There were three Formations in 1995 which held this 3-and-4 theme: a 'Double Vesica Pisces' in Wherwell, Hants consisted of 4 3-sided petals around a square; at the centre of the Vector Equilibrium (Winterbourne Bassett, Wilts) was a triangle, each of whose faces was also the face of a square, and each face of each square was also the face of an adjacent triangle - the VE presents a resolution of oddness and evenness, the YinYang of Three and Four; and finally, the next-to-last Formation of the year on the Avebury Avenue was one we'd seen (most of) before:
All lines should touch the Circles, and the Path to the bottom-most Circle begins on the cross-bar and slants a bit from left to right. We have seen the 3-Circles-in-a-Triangular pattern at least three times now, but this is the first time of which I'm aware that the fourth was added: a clear 3 --> 4.
The Five Circle Theorems are only the geometrical portion of the surprise Dr Hawkins received as he studied the Circles. He also realised that many of the numbers regularly turning up in his analyses were diatonic ratios. Diatonics are mathematical equivalents of musical notes as played, for example, on the white keys of a piano. Each of these newly recognised theorems involve diatonic ratios, which are based on the ratios of areas and diameters between the Circles. The only regular polygons whose circumscribed and inscribed circles are in diatonic (musically- or vibrationally-related) ratio are the triangle (3), square (4), and hexagon. Last year, the Oliver's Castle Formation (the focus of the extraordinary video footage one young man was Gifted with) depicted 6-fold geometry ...
All 'Laws' currently acknowledged by our scientists are in various stages of perpetual evolution, for our understanding of Natural Law is far from complete - in truth, it has hardly begun. As our understanding evolves, so we evolve the concepts within our Laws, for we are able to express greater portions of Truth through them as our own awareness and understanding expand. The Law is immutable. It is our understanding which grows as it accepts and assimilates Truth.
Our paths to enlightenment are initially roughed out by nudgings of curiosity within us. If we 'bite', our initial curiosity is followed by a surge of focused, single-minded determination (we begin to scratch the itch); our path becomes more clear; the more sustained our determination, the better we're able to resolve our itch to our satisfaction. Ultimately, if we've done our homework well, we are Gifted with a "Eureka!"-flash of Insight. The vibrational equivalent of this "Eureka!" synchronistically-generates an opening - an interdimensional doorway - through which the seeker has earned the right to retrieve a portion of Greater Reality Truth. It is this harmonic resonance between Seeker and Sought which, in fact, opens the transdimensional door ...
To retrieve pieces of Truth in this manner and ground them into 3rd density is precisely the reason we have incarnated upon this planet at this time. We decided to explore our consciousness' creativity at this very dense/slow frequency level for many reasons. There are great difficulties and pitfalls here, to be sure. But there are also incredible Gifts available as we succeed. By anchoring the higher Truths, or frequencies, into our third dimensional reality (as Dr Hawkins has done in this case) we are literally raising the frequency of our specie's collective consciousness. In a free will civilisation such as ours, the ramifications and benefits for all are immense.
An interesting metaphysical concept making the rounds today suggests that our species is undergoing a 'paradigm shift' or a 'shift in consciousness'. The symbolism used to describe it suggests that our vibratory frequencies are 'speeding up' as we move from the 3rd to the 4th density ...
While Dr Hawkins may not subscribe to density shifts ;-) the numbers he continues to turn up through his theorems are confirmed as well in other facets of the Circle Phenomenon. I do not believe in 'accidents' or 'coincidences'. Energies are set in motion through Intent of consciousness; the 'intersections' of such Energies-in-motion are hardly random or, worse, inconsequential. Rather, they are the very purpose behind consciousness' creative explorations!
Synchronicities are our Immediate Feedback Tools - they are the Universe's way of letting us know whether or not we're on-line with our Intentions ... ;-) That Professor Hawkins came upon these Theorems at this time was surely no accident ... nor was it 'coincidence' that his retrieval of these Truths came as he stepped through the transdimensional window generated by the Crop Circles ...
I'd be interested in your feedback on Dr Hawkins' work, or on any of my thoughts you might like to comment on ...
Thank you kindly!
- ilyes
May 30, 1997