“Overlapping triangle codes” as drawn in English crop pictures: the extra-terrestrials are teaching us a novel kind of mathematics, which they have used to encode numbers such 13, 26, 52 or 104 from Mayan calendars by Red Collie (Dr. Horace R. Drew, Caltech 1976-81, MRC LMB Cambridge 1982-86, CSIRO Australia 1987-2010)

“Overlapping triangle codes” as drawn in English crop pictures: the extra-terrestrials are teaching us a novel kind of mathematics, which they have used to encode numbers such 13, 26, 52 or 104 from Mayan calendars

Many novel kinds of mathematics have been drawn in English crop pictures, for example “pi to ten digits” at Barbury Castle on June 1, 2008 (see www.dailymail.co.uk or www.telegraph.co.uk). That puzzle was not solved for over a week, while images of the crop picture spread widely over the Internet to millions of people around the world. Finally Mike Reed, a retired astrophysicist living in North Carolina, realized what it meant, then informed Linda Howe and myself.

Here we will show four other mathematical puzzles which were drawn in crops during the summers of 2000, 2009 or 2012. No one has realized what they mean until now. They are all based on complex triangular geometries.

The first “triangle puzzle” to appear in crops was near Silbury Hill in June of 2000

The first “triangle puzzle” to appear in crops was drawn near Silbury Hill in June of 2000. It came down in two separate phases on June 2 then June 4:

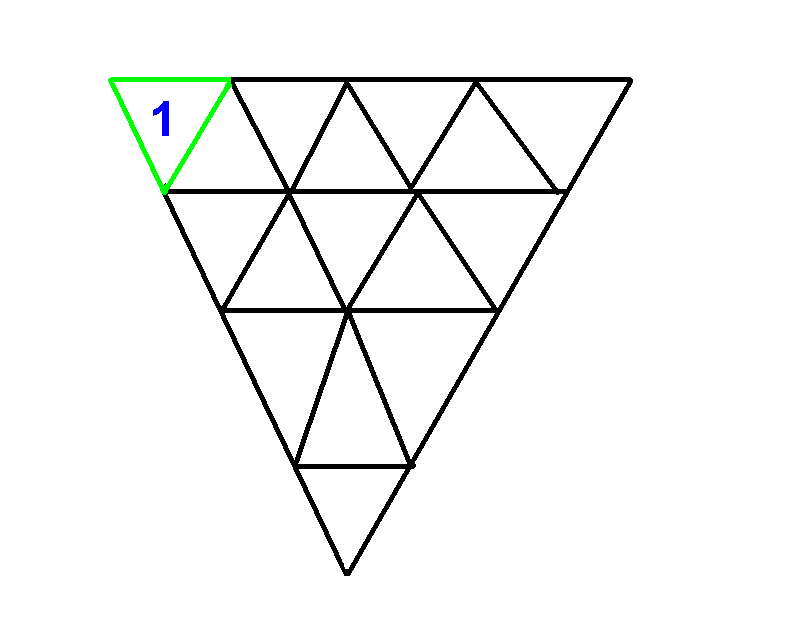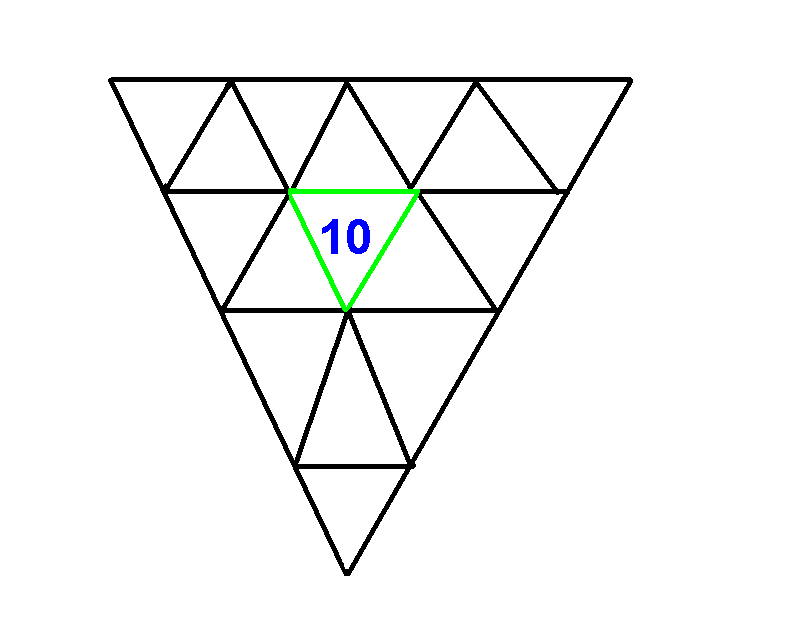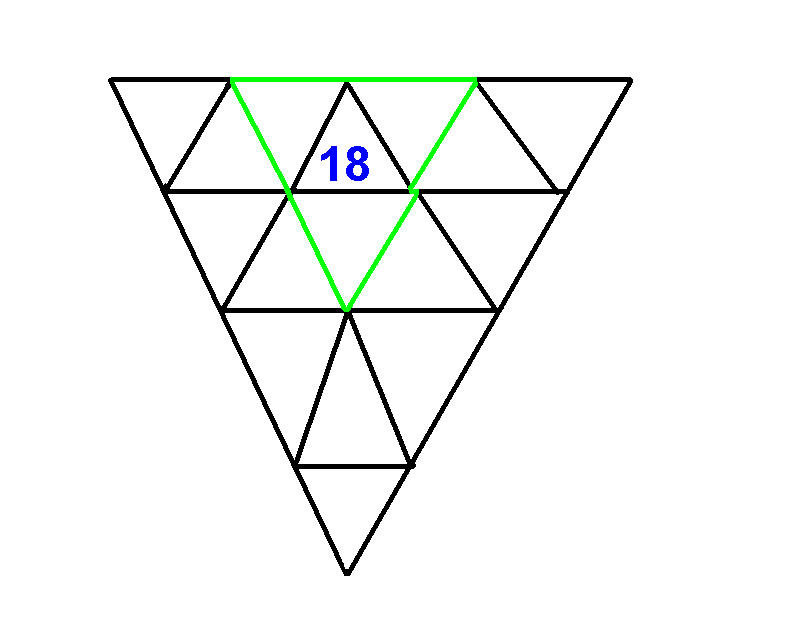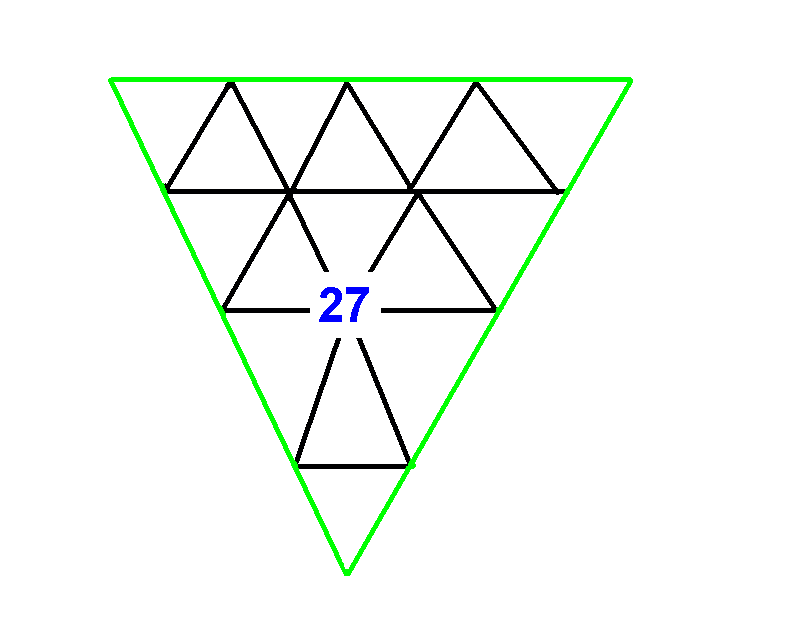
This puzzle relates the number of vertical levels in Pascal’s Triangle, to the number of small overlapping triangles which may be counted inside (see jwilson.coe.uga.edu). The crop picture shows an example for n = 3 and 13 triangles. Please study this clever animation to see the results for n = 4 and 27 triangles, which are directly comparable (see www.transum.org or http://krexy.com/how-many-triangles):

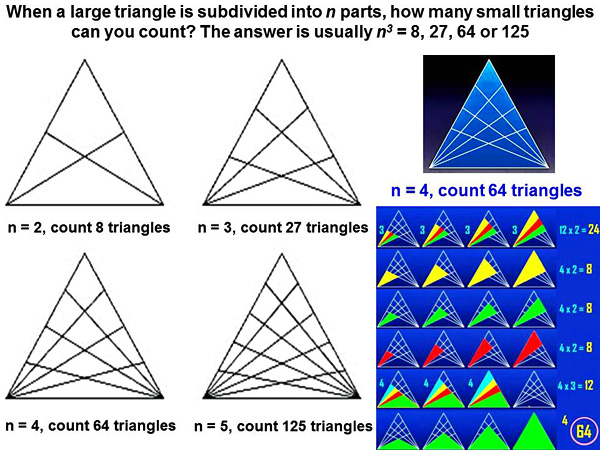
I am calling this “Pascal’s Triangle”, because we will return to that particular geometry in other slides below.

How many small triangles can we count within a large triangle that has been subdivided into n parts?

The next two “triangle puzzles” to be drawn in crops during 2009 or 2012 were more difficult to understand. In order to explain what they mean, first we need to show an example of overlapping triangular geometries. How many small triangles can you count, within a large triangle that has been subdivided into n parts?

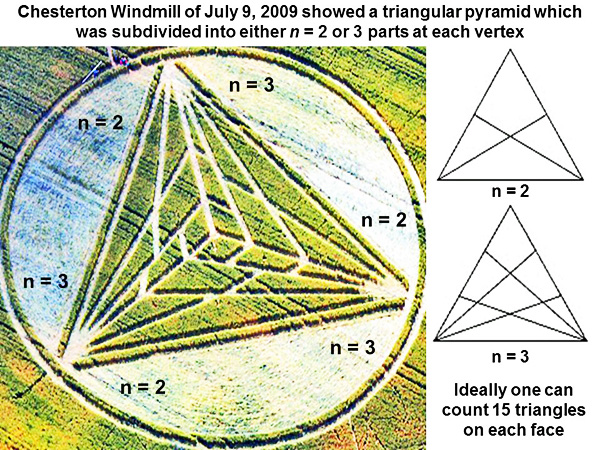
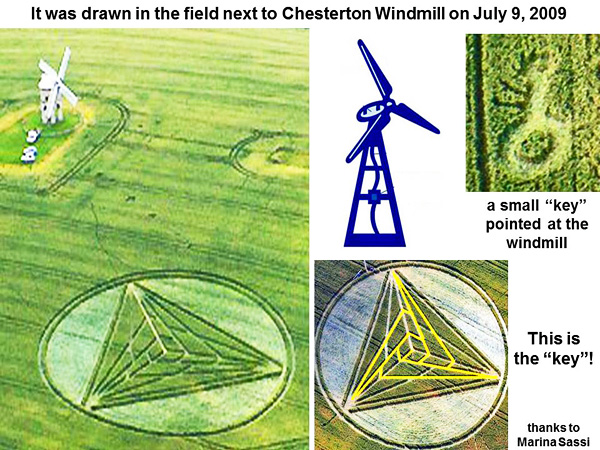
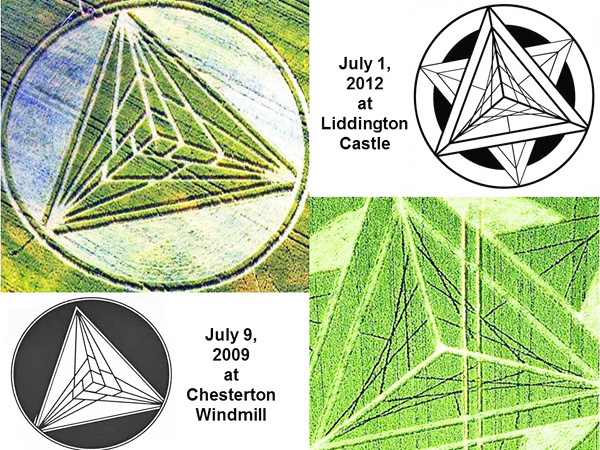
The answer is usually n cubed, for example 8 triangles for n = 2, or 27 triangles for n = 3, or 64 triangles for n = 4, or 125 triangles for n = 5 (see http://scienceblogs.com). The case of n = 4 is shown in detail on the right, where all 64 of its small, overlapping triangles are counted carefully.

A “triangular pyramid” which appeared in crops near Chesterton Windmill on July 9, 2009 was subdivided as n = 2 or n = 3 at different vertices

Now everything is going to get a bit harder! A “triangular pyramid” which appeared in crops near Chesterton Windmill on July 9, 2009 was subdivided on each face as n = 2 or n = 3 at different vertices:

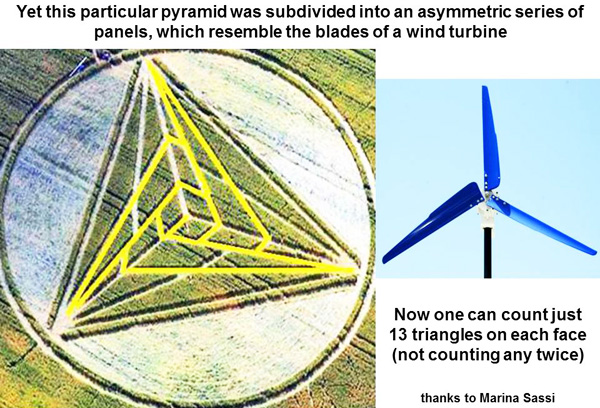
Ideally for this example, we might expect to count 15 overlapping triangles along each face, which is a value intermediate between 8 triangles for n = 2 at both vertices, or 27 triangles for n = 3 at both vertices. Yet the crop artist has some surprises in store! This particular pyramidal shape was subdivided into an asymmetric set of panels, which resemble the blades of a wind turbine:

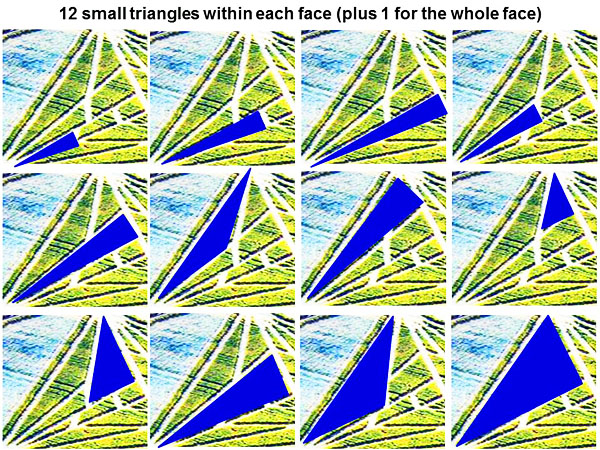
Now one can count just 13 triangles on each face, instead of the expected 15 for ideal symmetry:

There are 12 small triangles which subdivide each face. Then we must add one large triangle for the whole face, to give a total of 12 +1 =13.

This crop picture was drawn in a field near Chesterton Windmill, along with a small “key” motif which pointed towards the windmill. It showed six tiny lines on the top, which resemble a six-lined vertex from the triangular crop picture:

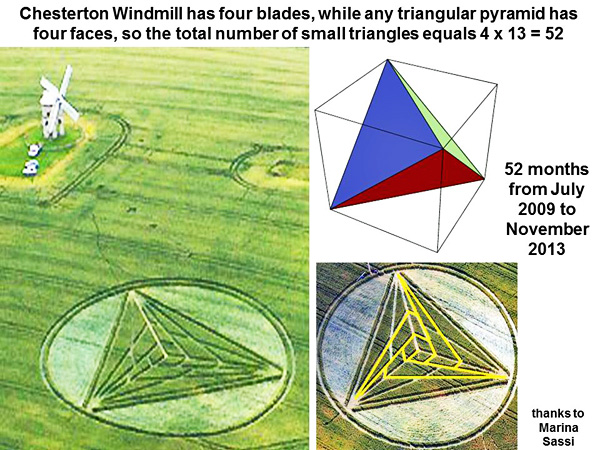
The “key” to understanding this puzzle is to realize that the triangular crop picture would possess four faces in three dimensions, just like the four blades of that windmill:

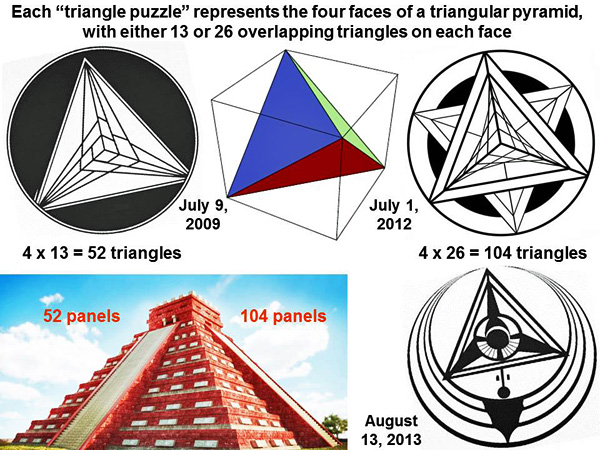
The total number of small, overlapping triangles therefore equals 4 x 13 = 52, even though a lower face of the pyramid with 13 triangles remains “hidden”. Could there be some intent here to refer to “52 months” which separate July 2009 and December 2013, the latter date of which has been coded in other crop pictures? (see /fringe2013k)

Those two coded numbers of “13” or “52” have distinct connotations in terms of ancient Mayan culture. There are 13 baktuns in one part of the Mayan Long Count calendar, while there are 52 panels on each face of the Pyramid of Quetzalcoatl in Chichen Itza:

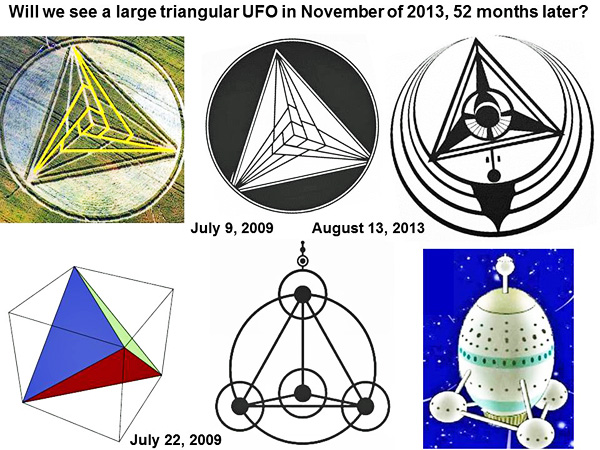
Those 52 panels on each face of the Mayan pyramid represent “52 years” in their Sun-Venus calendar. Once again, might the Chesterton Windmill crop picture be referring to the “52 months” between July 2009 to December 2013? Will we perhaps see a large triangular UFO then?

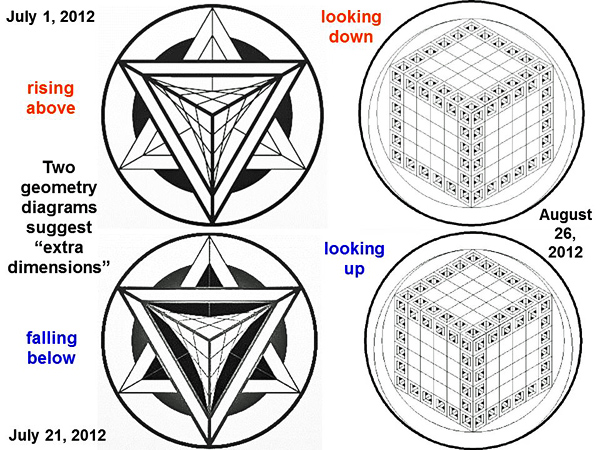
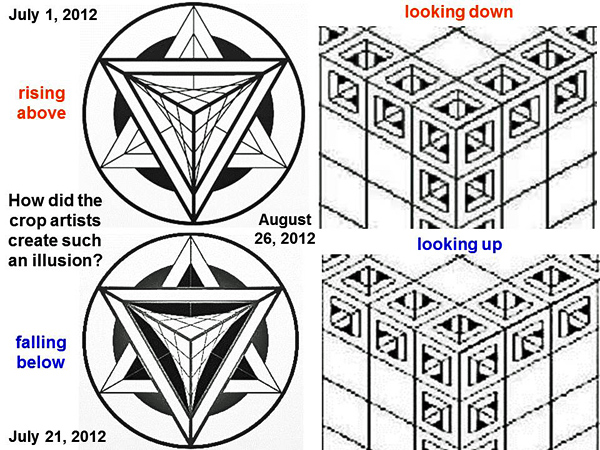
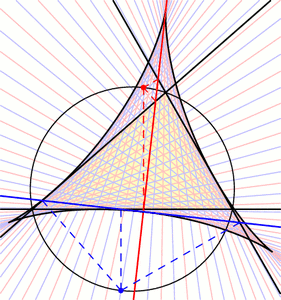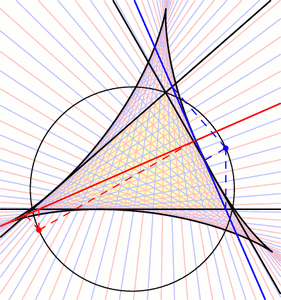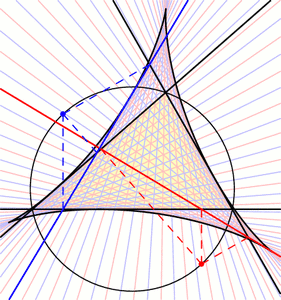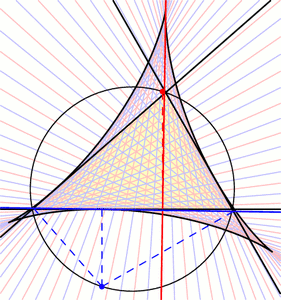
A “large triangular UFO” was drawn in crops at West Kennett Long Barrow on August 13, 2013. It looks much like the crop picture drawn at Chesterton Windmill on July 9, 2009. Later in the same month of July 2009, another “triangular pyramid” as drawn in crops also resembles a triangular or pyramidal UFO.

Two complex geometry diagrams from 2012 suggest “extra dimensions”

We will show other interesting “triangle puzzles” below, but first we need to prepare the way with further explanatory information. Two different geometry diagrams from the summer of 2012 suggested “extra dimensions”. The first at Liddington Castle on July 1, 2012 (then July 21) showed the image of a cube passing through our 3-D space from other dimensions (see fringe2013b):

In their first diagram on July 1, we can see one corner of that cube “rising above” the plane of the crop field. Then in their second diagram on July 21, we can see a corner of that cube “falling below” the plane of the crop field.

Later on August 26, 2012, they drew a very intricate 3-D cube which shows a similar change of perspective. We can apparently visualize the front corner of that cube by either “looking down” or “looking up” (see also hackpenhill3). How did the crop artists create such an amazing illusion? As shown in the next slide, they achieved this by changing the nature of visual perspective in its central parts:

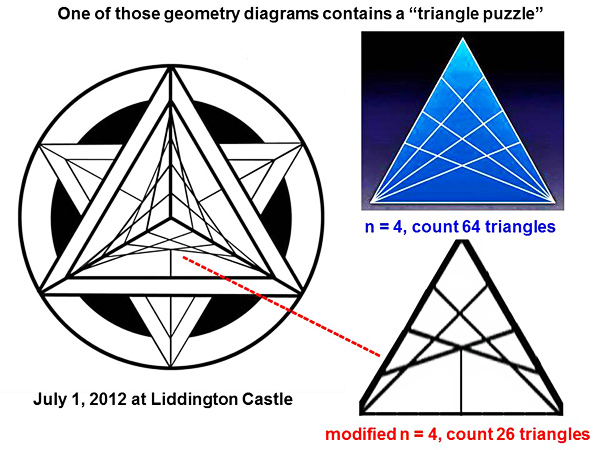
One of those complex geometry diagrams contains another “triangle puzzle”

Now quite remarkably, one of those geometry diagrams from the summer of 2012 also contains a “triangle puzzle”, like the example from Chesterton Windmill which we just studied above. We will be able to study this new triangle more easily if we “stretch” it away from the curved shape drawn in crops, back into a simple linear shape:

This new triangle is a clever variation away from the idealized case of n = 4 as discussed above, which contains 64 small, overlapping triangles. In this new case, line 1 remains the same, but lines 2 and 3 which subdivide the triangle are connected differently to their opposite sides. When we count carefully, we find that the modified n = 4 triangle contains only 26 overlapping triangles, instead of 64 as for the ideal case:

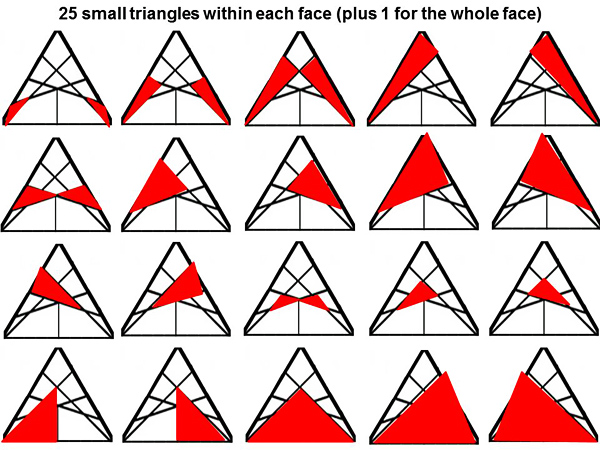
Again we can count 25 small, overlapping triangles within each face. Then we need to add one more for the whole face to reach a total of 25 + 1 = 26.

One small line near the centre of the triangle has been subtly omitted, or else we would find a total of 30 triangles rather than 26.

Finally, in order to switch our linearized triangle back into its curved shape as was drawn in crops, we can apply a mathematical method known as “Steiner’s deltoid” (see /blog.zacharyabel.com):

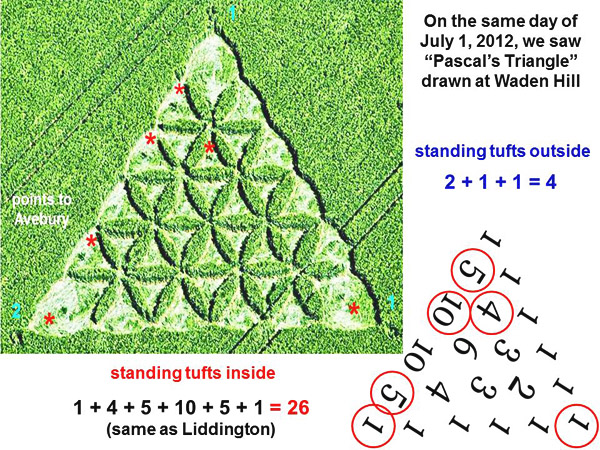
The highly curved triangle which was drawn in crops appears “hyperbolic”, in order to symbolize a hyperbolic spatial geometry for “extra dimensions”.

Pascal’s Triangle with a code for “26 triangles” appeared in crops at Waden Hill on the same day of July 1, 2012

During the day of July 1, 2012, we were inspecting a new crop picture near Stanton St. Bernard with Paul Jacobs and Stuart Dike. Then a call came in, to inform us that a new crop picture had just been found on top of Waden Hill, not far from Avebury or Silbury Hill. When we arrived there, the new crop picture was still pristine, because only three people were in it on the ground.

One was Ross Holcombe, who was busy sketching a complex code which he had found. Six of its 36 triangular spaces showed standing tufts, while the other 30 spaces showed centres which were swirled just slightly off the ground. In the slide below, we have added six “red asterisks” to denote where six standing tufts of crop were located:

Once we saw an aerial photograph, we realized that the Waden Hill crop picture shows “Pascal’s Triangle”, using the artistic style for a “flower of life”. The total number of triangular spaces on each level of the triangle equalled 1, 3, 5, 7, 9 or 11. Yet when studied in the form of Pascal’s Triangle, only 1, 2, 3, 4, 5 or 6 spaces on each level were available for coding. Those six standing tufts match individual numbers of 1, 4, 5, 10, 5 or 1 from Pascal’s Triangle, and add to a total of 26.

Now the other crop picture which appeared at Liddington Castle on July 1, 2012 also showed “26 triangles”, within each face of a triangular pyramid. Could the coded triangle at Waden Hill have been meant to help us read a different coded triangle at Liddington? Most of the individual numbers at Waden Hill match the number of small triangles of each kind, which were drawn on the same day at Liddington: 10 triangles based on the lowest pair of subdividing lines, 6 (or 5 +1) triangles based on the middle pair of subdividing lines, 4 triangles based on the highest pair of subdividing lines, 5 symmetric triangles in the centre, and 1 large triangle for the entire face.

Around the outside of Waden Hill, we can see 2, 1 or 1 standing tufts which add to 4. Might those four outer tufts represent the four faces of a triangular pyramid which was drawn at Liddington?

Comparing the triangle puzzle from Chesterton Windmill 2009 with a triangle puzzle from Liddington Castle 2012

When we compare both crop pictures as seen from above, their similarities become striking:

Both crop pictures show large triangular pyramids, which have been coded on each face with either 13 or 26 small, overlapping triangles. When viewed in three dimensions, each triangular pyramid would possess four faces.

We may summarize our current results as follows:

The triangle puzzle from Chesterton Windmill on July 9, 2009 shows 4 x 13 = 52 small, overlapping triangles. The triangle puzzle from Liddington Castle on July 1, 2012 shows 4 x 26 = 104 small, overlapping triangles. Both of those numbers “52” or “104” match the number of panels found on one or two faces of the Pyramid of Quetzalcoatl in Chichen Itza. Both crop pictures also resemble a “large triangular UFO”, which was drawn in crops at West Kennett Long Barrow on August 13, 2013.

Who knows what will happen next? All of these spectacular field images must be leading somewhere. The past is prologue.

Red Collie (Dr. Horace R. Drew, Caltech 1976-81, MRC LMB Cambridge 1982-86, CSIRO Australia 1987-2010)

P.S. We would like to thank Marina Sassi for the “yellow windmill” image of a crop picture at Chesterton Windmill on July 9, 2009, and also Sarah Susanka for her careful analysis of the “cube” from Hackpen Hill on August 26, 2012 (see hackpenhill3 or Sarah_Susanka):

“As an architect, I draw window frames in perspective all of the time. So it is very apparent to me that the way in which these lines of see-through cubes have been drawn is actually ‘upside-down and inside-out’, relative to what our eyes would expect to see at the upper, outward-pointing corner of the cube. This tells me that we are being shown an upside-down world beyond the boundaries of that cube, or on its other side.”

Indeed, the crop artists seem to come from a “mirror universe” which is upside-down relative to ours (see fringe2013k). If an architect and best-selling author such as Sarah can get it right, why not the scientists or academics in our schools? As Joni Mitchell sings in “Shine”, they have tunnel vision (see www.youtube.com).